Изведување на состојбата $E(t)$ → Изложени (Еxposed)
Многу заразни болести имаат инкубациски период пред да станат заразни, период додека домаќинот (host) сеуште не може да го шири вирусот. Во овој модел овие индувидуи ги нарекуваме изложени, а состојбата ја означуваме со $E(t)$.
Интиутивно, ќе имаме транзиции помеѓу состојби од следниот облик:
\begin{align*} S\rightarrow E\rightarrow I \rightarrow R \end{align*}Подлежни луѓе кога стапуваат во контакт со вирусот транзитираат во состојба изложени, кои по инкубацискиот период транзитираат во инфицирани и по своето заздравување транзитираат во оздравени.
Оваа нова транзиција што се додава на овој SEIR модел, е таа од облик $S \rightarrow E$, која ја поседува истата насока на транзитирање како и таа во претходниот модел $S \rightarrow I$, за која:
- веројатноста е еквивалентна со веројатноста од транзицијата $S \rightarrow I$(сите подлежни може да бидат изложени)
- стапката на пренесување а исто еквивалентна од транзицијата $S \rightarrow I$ (изложеноста настанува веднаш)
- популацијата е исто еквивалентна од транзицијата $S \rightarrow I$, бидејќи заразени индивидуи можат да ја шират болеста и секој еден од нив ја изложува на $\beta$ личности на ден
Истотака нема потреба за промена во транзицијата од $I \rightarrow R$. Единствената нова транзиција што се додава е таа од $E \rightarrow I$ за која:
- веројатноста е 1 (сите што се изложени транзитираат во инфицирани)
- стапката на пренесување добива нова нотација $\delta$ (делта)
- популацијата е еднаква на $E$ (сите изложени ќе транзитираат во инфицирани)
Се добиваат следните состојби со равенки:
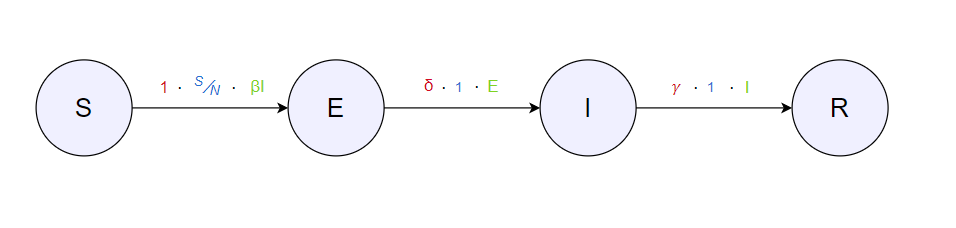
Од овие транзиции ги изведуваме следните равенки:
\begin{align*} \frac{dS}{dt} &= -\beta \cdot I \cdot \frac{S}{N} \\ \frac{dE}{dt} &= \beta \cdot I \cdot \frac{S}{N} - \delta \cdot E \\ \frac{dI}{dt} &= \delta \cdot E - \gamma \cdot I \\ \frac{dR}{dt} &= \gamma \cdot I \end{align*}Програмирање на состојбата $E(t)$ → Изложени (Еxposed)
Програмирањето на оваа состојба е доста директно. Ќе моделираме сценарио со многу голема рата на заразување ($R_0=5.0$) на 1 милион популација, со инкубациски период од 5 изминати денови и стапка на оздравување 7 денови.
Графикот за вредностите на $S, E, I, R$ во тек од 100 денови:
# Python3 imports
from scipy.integrate import odeint
import numpy as np
import math
import plotly.graph_objects as go
import plotly.tools as tls
from plotly.offline import plot, iplot, init_notebook_mode
from IPython.core.display import display, HTML
init_notebook_mode(connected = True)
config={'showLink': False, 'displayModeBar': False}
def deriv(y, t, N, beta, gamma, delta):
S, E, I, R = y
dSdt = -beta * S * I / N
dEdt = beta * S * I / N - delta * E
dIdt = delta * E - gamma * I
dRdt = gamma * I
return dSdt, dEdt, dIdt, dRdt
N = 1_000_000
D = 3.0 # infections lasts four days
gamma = 1.0 / D
delta = 1.0 / 5.0 # incubation period of five days
R_0 = 5.0
beta = R_0 * gamma # R_0 = beta / gamma, so beta = R_0 * gamma
S0, E0, I0, R0 = N-1, 1, 0, 0 # initial conditions: one exposed
t = np.linspace(0, 99, 100) # Grid of time points (in days)
y0 = S0, E0, I0, R0 # Initial conditions vector
# Integrate the SIR equations over the time grid, t.
ret = odeint(deriv, y0, t, args=(N, beta, gamma, delta))
S, E, I, R = ret.T
# Plot Model using plotly
figa = go.Figure()
figa.add_trace(go.Scatter(x = t,
y = S,
mode = 'lines',
line=dict(color="blue",
width=2),
name = "Подлежни; <i>S(t)</i>",
hovertemplate = '<i> %{y:.0f} </i> луѓе'))
figa.add_trace(go.Scatter(x = t,
y = E,
mode = 'lines',
line=dict(color="#CCCC00",
width=2),
name = "Изложени; <i>E(t)</i>",
hovertemplate = '<i> %{y:.0f} </i> луѓе'))
figa.add_trace(go.Scatter(x = t,
y = I,
mode = 'lines',
line=dict(color="red",
width=2),
name = "Заразени; <i>I(t)</i>",
hovertemplate = '<i> %{y:.0f} </i> луѓе'))
figa.add_trace(go.Scatter(x = t,
y = R,
mode = 'lines',
line=dict(color="green",
width=2),
name = "Оздравени; <i>R(t)</i>",
hovertemplate = '<i> %{y:.0f} </i> луѓе'))
figa.add_trace(go.Scatter(x = t,
y = list(S+E+I+R),
mode = 'lines',
line=dict(color="#ade6e6",
width=2,
dash="dash"),
name = "Вкупно",
hovertemplate = '<i> %{y:.0f} </i> луѓе'))
figa.update_layout(title = 'SЕIR модел',
title_x = 0.5,
xaxis_title='t',
xaxis=dict(range=[0,100],
mirror=False,
ticks='outside',
showline=True,
tickvals = [0, 20, 40, 60, 80, 100],
linecolor='#000',
tickfont = dict(size=11)),
yaxis_title='Број на луѓе',
yaxis=dict(range=[0,1100000],
mirror=False,
ticks='outside',
showline=True,
showspikes = True,
linecolor='#000',
tickvals = [0, 200000, 400000, 600000, 800000, 1000000],
tickfont = dict(size=11)),
plot_bgcolor='#fff',
hovermode = 'x unified',
width = 650,
height = 320,
font = dict(size = 10),
margin=go.layout.Margin(l=50,
r=50,
b=60,
t=35))
plot(figa, filename = 'fig3_a.html', config = config)
display(HTML('fig3_a.html'))
Сега го доведовме најосновниот SIR модел до степен каде можеме малку пореалистично да разгледуваме вистински заразни болести. Меѓутоа дефинитивно сеуште фали една многу битна состојба, бројот на починати.
