SIR за data-fitting
Градиме модел изведен од последните неколку тетратки: Луѓето од популацијата се прво Подлежни- можат да го фатат вирусот (веројатност $\frac{S}{N}$) и постануваат Изложени. Тие не можат да го шират сеуште вирусот. По неколку денови (поточно $\frac{1}{\delta}$) тие транзитираат во состојба Инфицирани и го шират вирусот. Додека се заразени можат или да транзитираат во состојба Починати (по $\frac{1}{\rho}$ денови со веројатност $\alpha$) или да транзитираат во состојба Оздравени (по $\frac{1}{\gamma}$ денови):
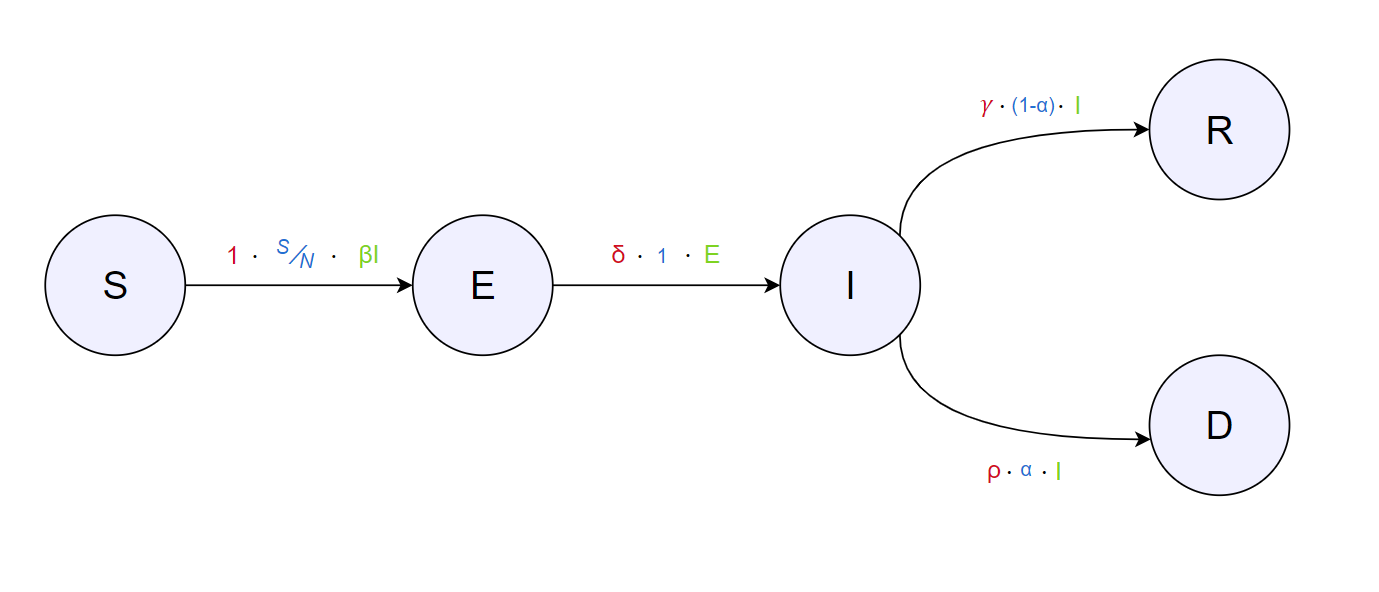
Да направиме едно мало навраќање, овие се променливите кои се дел од равенките:
- $N$: вкупна популација
- $S(t)$: број на подлежни луѓе на ден $t$
- $E(t)$: број на изложени луѓе на ден $t$
- $I(t)$: број на инфицирани луѓе на ден $t$
- $R(t)$: број на оздравени луѓе на ден $t$
- $D(t)$: број на починати луѓе на ден $t$
- $\beta$: очекуваниот број на луѓе на кои заразена личност ја пренесува болеста
- $D$: бројот на денови што личноста ја чува во себе и може да ја шири болеста
- $\gamma$: дел од заразени личности што заздравуваат на ден ($\gamma= \frac{1}{D}$)
- $R_{0}$: вкупниот број на луѓе кој една личност заразува ($R_{0}=\beta \cdot D$)
- $\delta$: времетраење на инкубациски период
- $\alpha$: стапка на смртност (дел од заразените што починуваат, се среќава во литература како fatality rate)
- $\rho$: стапката на денови за еден заразен да почине (=1/денови од заразен до смрт)
На овој модел додаваме само уште една нова состојба, таа е $C(t) - $ Критични (Critical). Оваа состојба ја сочинуваат личности што им е потребна интензивна нега, овозможувајќи ни на нас да додаеме малку повеќе реалност на моделирањето со воведување на "преполовување" на болници како резултат на недостаток од ресурси. Секако во оваа состојба би транзитирале личности кои се претходно Заразени, од оваа состојба повторно тие или ќе транзитираат во Починати или во Оздравени.
Оваа нова поставеност подига нови прашања за кои се всушност вредностите кои овие транзиции ќе ги добијат. Ќе се обидеме да ги објасниме како ние ги разбравме. Нас ни е потребна веројатноста дека еден заразен човек ќе стане критичен случај. За да не додаваме нови имиња и ознаки на параметри за да не ни се прави гужва во равенките ние за оваа веројатност ќе користиме нотацијата: $P(I\rightarrow C)$, што е веројатноста еден заразенда транзитира во критичен.
Сега, имајќи ја оваа веројатност ни е потребна истотака и веројатноста дека еден критичен човек транзитира во починати, т.е. веројатноста дека некој може да почине додека е во критична здраствена состојба: $P(C\rightarrow D)$. Пропорционално на ова, според правилото за одзима на веројатности [4]:
\begin{align*} \tag{Rule of Subtraction} P(A) &= 1-P(\bar{A}) \end{align*}следува дека веројатноста од за транзиција од состојба заразен во состојба оздравен е: $P(I\rightarrow R) = 1 - P(C\rightarrow D)$. Единствените бројки кои ни остануваат за дијаграмот на состојби се:
- стапката на луѓе кои стануваат критични (од заразени во критични)
- стапката на луѓе кои починуваат додека се критични (од критични во починати)
- стапката на луѓе кои оздравуваат додека се критични( од критични во оздравени)
Овие рати (стапки) кружат околу интернетот, секако можеби има поточни вредности:
- Бројот на денови од заразен во критичен: 12 ( → стапка: 1/12)
- Бројот на денови од критичен во починат: 7.5 ( → стапка: 1/7.5)
- Бројот на денови од критичен во оздравен: 6.5 ( → стапка: 1/6.5)
Доколку го "допрошириме" моделот на транзиции од претходната фигура, се добива:
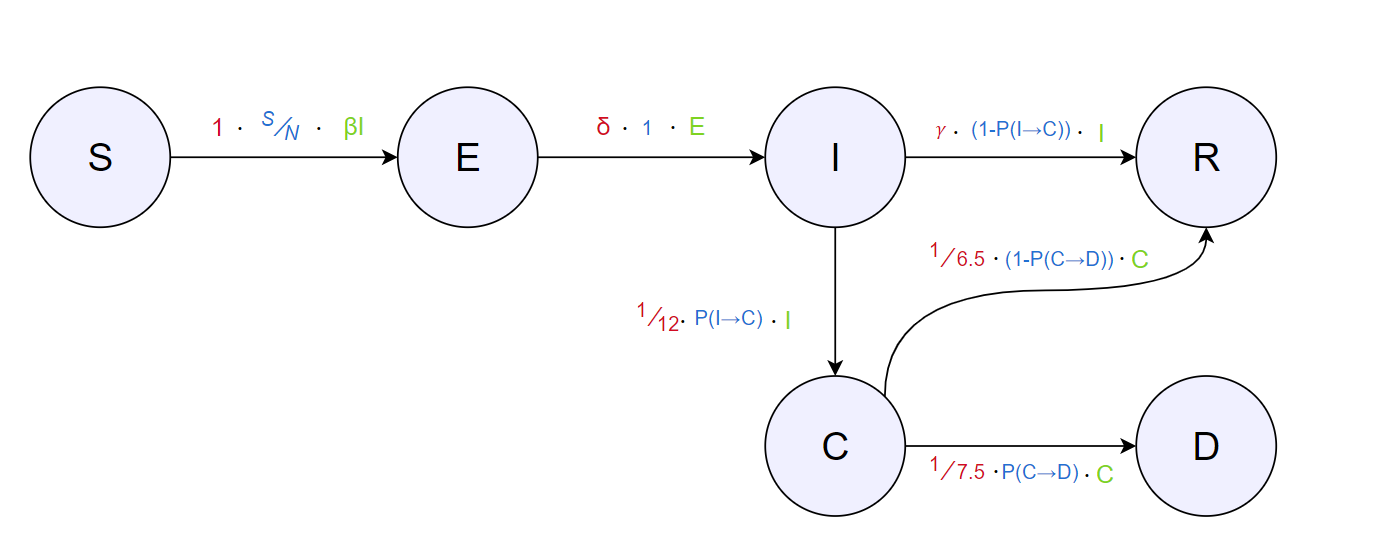
Недостиг на ресурси
Како резултат на недостиг од доволно развиени алатки за мониторирање на ефектите од заштитните мерки, вклучувајќи ги социјалното дистанцирање и прогнозирањето на пандемии е од неизмерен интерес со избивањето на COVID-19 [5] 30627-9/fulltext)[6]. Вистинските податоци се доста непрецизини (како резултат на шум) и често се оштетени од неадекватни системи на државите за системи кои точно зачувуваат податоци. Изминатите неколку месеци има голем број на трудови кои го покриваат делот како тријажата (triage) се третира во Италија и други земји и места кои беа силно погодени од вирусот, поточно доктори кои биле во ситуација да одлучуваат кои да третираат со ограничените болнички капацитети.
Ова може да се приклучи на нашиот претходен проширен SIR модел на следниот начин:
Замислуваме дека одредена земја со $B$ кревети за интензивна нега соодведни да третираат личности кои се критични со COVID-19. Доколку има повеќе од $B$ критично болни личности (состојбата $C>B$), сите луѓе што се над $B$, на пример доколку $B=500$ илјади, $C=600$ илјади, тогаш 100 илјади луѓе не се третираат поради недостиг на ресурси.
Ова значи дека $C-B$ луѓе умираат поради недостиг на ресурси. Секако обратното сценарио каде имаме поголем број на кревети од критично заразени тогаш немаме проблем со недостиг на ресурси. Ова нотациски го бележиме со $max(0, C-B)$, бидејќи кога $B>C$ разликата е негативен број. На овој начин имаме $max(0, C-B)$ луѓе кои умираат поради недостиг на услови, или е 0 или е број поголем (нема логика да е негативен број). Со ова на ум сега можеме уште еднаш да ги дополниме транзициите во дијаграмот на состојби.
Прошируваме на следниот начин: од $C$ (критични), има две популации кои ги зимаме во предвид: $max(0, C-B)$ луѓе умираат од недостиг и останатите што се третираат. Кои се останатите? Ако $C<B$ (доволно кревети), тогаш $C$ луѓе се третираат. Доколку $B>C$ (недостиг кревети) тогаш $B$ луѓе се третираат. Тоа значи дека "останатите" - се луѓето што добиваат третман што е всушсност $min(B,C)$. Повторно доколку $C<B$, минимумот е $C$ луѓе се третираат, обраниот $C>B$ минумумот е $B$ луѓе се третираат.
Конечно доаѓаме до поправниот проширен модел (каде смрт настанува веднаш доколку дојде до недостиг, некои модели оваа веројатност ја моделираат на пр со 75% или сл.):
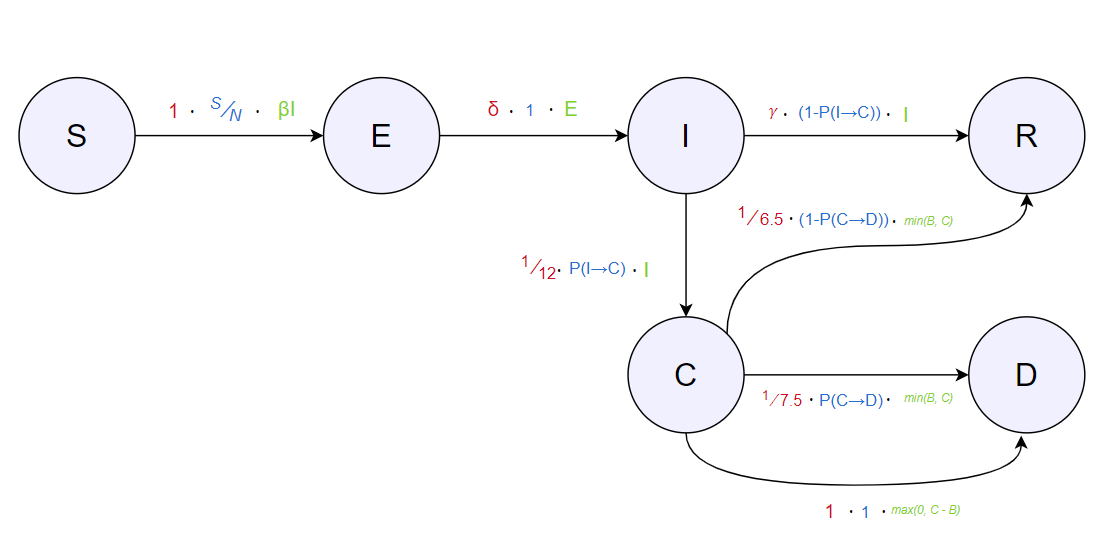
Овие се равенките кои соодвестуваат на овој модел:
\begin{align*} \frac{dS}{dt} &= -\beta (t) \cdot I \cdot \frac{S}{N} \\ \frac{dE}{dt} &= \beta (t) \cdot I \cdot \frac{S}{N} - \delta \cdot E \\ \frac{dI}{dt} &= \delta \cdot E - \gamma \cdot (1-P(I\rightarrow C)) \cdot I - \frac{1}{12} \cdot P(I\rightarrow C) \cdot I\\ \frac{dC}{dt} &= \frac{1}{12} \cdot P(I\rightarrow C) \cdot I - \frac{1}{7.5} \cdot P(C\rightarrow D) \cdot min(Beds(t), C) - max(0,C-Beds(t)) - \frac{1}{6.5} \cdot (1 - P(C\rightarrow D)) \cdot min(Beds(t), C) \\ \frac{dR}{dt} &= \gamma \cdot (1 - P(I\rightarrow C)) \cdot I + \frac{1}{6.5} \cdot (1 - P(C\rightarrow D)) \cdot min(Beds(t), C)\\ \frac{dD}{dt} &= \frac{1}{7.5} \cdot P(C\rightarrow D) \cdot min(Beds(t), C) + max(0, C - Beds(t)) \end{align*}Забелешка: Вредноста на бројот на кревети, $Beds(t)$ е функција од време
Временски зависни Променливи
За овој модел, имаме само 2 временски зависни променливи:
- $R_0(t)$, од која следи $\beta (t)$ од $R_0=\frac{\beta}{\gamma}$
- $Beds(t)$ - бројот на кревети за интензивна како функција од време
За $R_0$, повторно ќе ја користиме истата logistic функција:
\begin{align*} R_0(t) &= \frac{R_{0_{start}}-R_{0_{end}}}{1+e^{-k\cdot (-x+x_0)}} + R_{0_{end}} \end{align*}Параметрите се:
$R_{0_{start}}$ и $R_{0_{end}}$ се вредностите за $R_0$ за првиот и последниот ден
$x_0$ е вредноста на x-оска за која $R_0$ има најстрмниот пад (inflection point, може да биде "главниот" ден кога е воведен карантин)
$k$ контролира колку брзо паѓа $R_0$
За параметарот $Beds(t)$, идејата е се додека вирусот се шири, земјите кои се на удар градат болници → поголем број на кревети слободни. Едноставен начин за да се моделира бројот на кревети е:
Каде $Beds_0$ е вкупниот број на кревети на почетокот од пандемијата и $f$ е некој фактор. Според формулата бројот на кревети се зголемува фактор по иницијалниот број секој ден (пример: $s=0.5$, на ден $t=50$, вредноста на $Beds(t)=2\cdot Beds_0$)
