Извеудвање на состојба $D(t)$ → Починати (Dead)
За заразни болести кои имаат превисоки стапки на смртност оваа состојба е можеби и од најголемо значење. Во моделирање на вакви заразни болести некогаш се додаваат комплетно различни состојби и различна динамика (разгледување на бројот на новородени за време на пандемија, смрттни случаеви кои не се повразни со болеста и сл.). Овие модели можат да стнаат и стануваат се поголеми и потешки кога станува збор за предвидување, бидејќи додавањето на овие нови состојби и параметри можеби одговара на една држава меѓутоа тој модел со тие состојби може да дава комплетно грешни резултати за друга држава.
Нашата моментална поставеност на транзициите меѓу состојби:
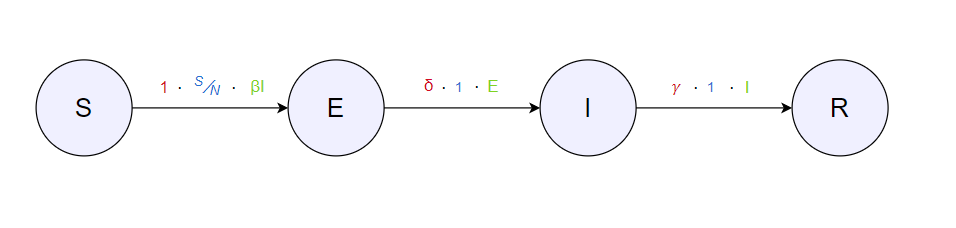
При додавање на нова состојба многу е важно да се разгледуваат моменталните транзиции и да се согледа каде состојбата што сакаме да ја додадеме има влијание или од која состојба зависи. За нашата нова состојба, $D(t)$, се прашуваме:
Одговорот е доста јасен: само откако ќе се заразат. Откако една личност ќе се зарази тој или оздравува или починува. Што следува дека нашата нова транзиција ќе биде од облик $I \rightarrow D$.
Се разбира дека смртта не настапува веднаш штом една личност ќе се зарази, за го моделираме ова време воведуваме нов параметар:
$\rho$: стапката на денови за еден заразен да почине
На пр. доколку се потребни 10 денови за еден заразен да почине, тогаш $\rho = \frac{1}{10} = 10 \% $.
Единствената работа што недостасува за комплетен модел со транзиции меѓу состојби се веројатностите за транзиција од инфициран во оздравен и од инфициран во починат. За ова ни е потребен параметарот:
$\alpha$: стапка на смртност (дел од заразените што починуваат)
На пр. нека $\alpha=5\%$, $\rho=1$ и $\gamma=1$ (луѓе починуваат или оздравуваат за 1 ден) и доколку на почетокот 100 луѓе се заразени, тогаш $5\% \cdot 100 = 5$ личности ќе транзитираат во починати, т.е. остануваат $95 \% \cdot 100=95$ личности ќе транзитираат во оздравени. Имајќи се во предвид, веројатноста за транзицијата $I \rightarrow D$ е еквивалентна на $\alpha$, додека веројатноста за транзицијата $I\rightarrow R$ е еквивалентна на $(1-\alpha)$.
Нашиот нов модел добива нов изглед на транзиции меѓу состојби:
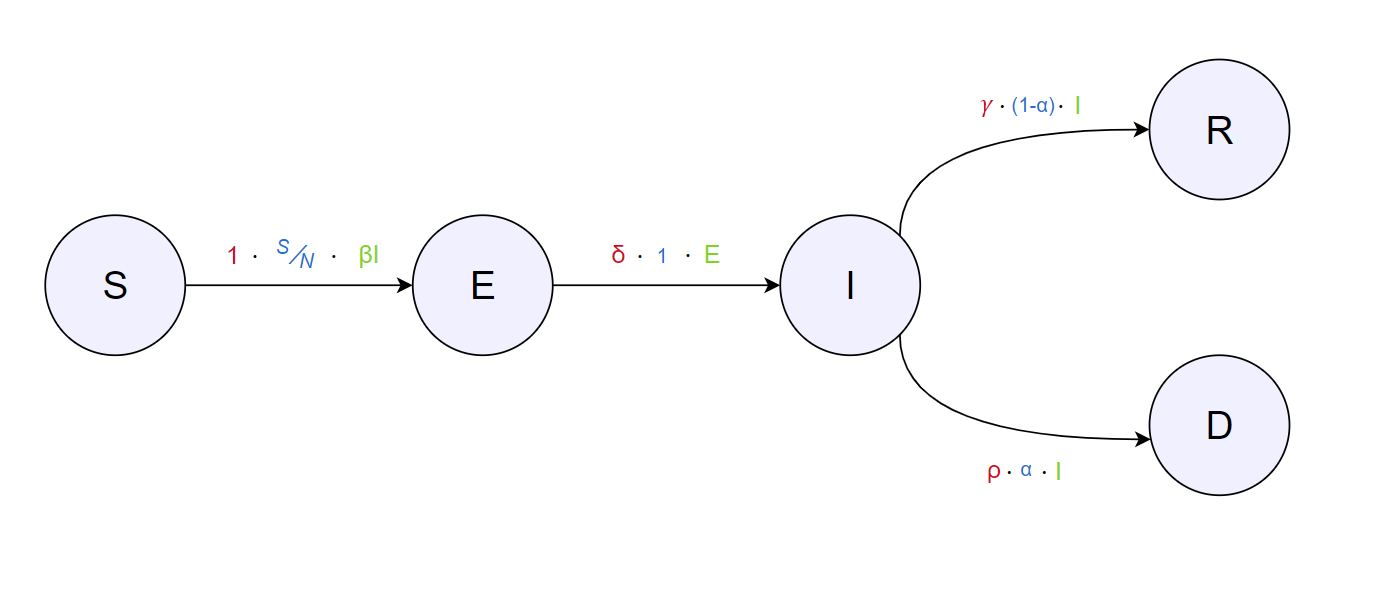
Од кои се изведуваат следните равенки:
\begin{align*} \frac{dS}{dt} &= -\beta \cdot I \cdot \frac{S}{N} \\ \frac{dE}{dt} &= \beta \cdot I \cdot \frac{S}{N} - \delta \cdot E \\ \frac{dI}{dt} &= \delta \cdot E - \gamma \cdot (1-\alpha) \cdot I - \rho \cdot \alpha \cdot I\\ \frac{dR}{dt} &= \gamma \cdot (1 - \alpha) \cdot I \\ \frac{dD}{dt} &= \rho \cdot \alpha \cdot I \end{align*}Со минимални промени од програмирањето на SEIR, додаваме иницијални вредности:
- $\delta = \frac{1}{5}$, инкубациски период
- $\alpha =$ 30%, стапка на смртност
- $\rho = \frac{1}{14}$, 14 дена од заразување до смртта
Се добива следниот графикон:
# Python3 imports
from scipy.integrate import odeint
import numpy as np
import math
import plotly.graph_objects as go
import plotly.tools as tls
from plotly.offline import plot, iplot, init_notebook_mode
from IPython.core.display import display, HTML
init_notebook_mode(connected = True)
config={'showLink': False, 'displayModeBar': False}
def deriv(y, t, N, beta, gamma, delta, alpha, rho):
S, E, I, R, D = y
dSdt = -beta * S * I / N
dEdt = beta * S * I / N - delta * E
dIdt = delta * E - (1 - alpha) * gamma * I - alpha * rho * I
dRdt = (1 - alpha) * gamma * I
dDdt = alpha * rho * I
return dSdt, dEdt, dIdt, dRdt, dDdt
N = 1_000_000
D = 3.0 # infections lasts four days
gamma = 1.0 / D
delta = 1.0 / 5.0 # incubation period of five days
R_0 = 5.0
beta = R_0 * gamma # R_0 = beta / gamma, so beta = R_0 * gamma
alpha = 0.3 # 30% death rate
rho = 1/14 # 14 days from infection until death
S0, E0, I0, R0, D0 = N-1, 1, 0, 0, 0 # initial conditions: one exposed
t = np.linspace(0, 99, 100) # time points
y0 = S0, E0, I0, R0, D0 # initial conditions vector
# Integrate the SIR equations over the time grid, t.
ret = odeint(deriv, y0, t, args=(N, beta, gamma, delta, alpha, rho))
S, E, I, R, D = ret.T
# Plot Model using plotly
figb = go.Figure()
figb.add_trace(go.Scatter(x = t,
y = S,
mode = 'lines',
line=dict(color="blue",
width=2),
name = "Подлежни; <i>S(t)</i>",
hovertemplate = '<i> %{y:.0f} </i> луѓе'))
figb.add_trace(go.Scatter(x = t,
y = E,
mode = 'lines',
line=dict(color="#CCCC00",
width=2),
name = "Изложени; <i>E(t)</i>",
hovertemplate = '<i> %{y:.0f} </i> луѓе'))
figb.add_trace(go.Scatter(x = t,
y = I,
mode = 'lines',
line=dict(color="red",
width=2),
name = "Заразени; <i>I(t)</i>",
hovertemplate = '<i> %{y:.0f} </i> луѓе'))
figb.add_trace(go.Scatter(x = t,
y = R,
mode = 'lines',
line=dict(color="green",
width=2),
name = "Оздравени; <i>R(t)</i>",
hovertemplate = '<i> %{y:.0f} </i> луѓе'))
figb.add_trace(go.Scatter(x = t,
y = D,
mode = 'lines',
line=dict(color="#696969",
width=2),
name = "Починати; <i>D(t)</i>",
hovertemplate = '<i> %{y:.0f} </i> луѓе'))
figb.add_trace(go.Scatter(x = t,
y = list(S+E+I+R+D),
mode = 'lines',
line=dict(color="#ade6e6",
width=2,
dash="dash"),
name = "Вкупно",
hovertemplate = '<i> %{y:.0f} </i> луѓе'))
figb.update_layout(title = 'SЕIRD модел',
title_x = 0.5,
xaxis_title='t',
xaxis=dict(range=[0,100],
mirror=False,
ticks='outside',
showline=True,
tickvals = [0, 20, 40, 60, 80, 100],
linecolor='#000',
tickfont = dict(size=11)),
yaxis_title='Број на луѓе',
yaxis=dict(range=[0,1100000],
mirror=False,
ticks='outside',
showline=True,
showspikes = True,
linecolor='#000',
tickvals = [0, 200000, 400000, 600000, 800000, 1000000],
tickfont = dict(size=11)),
plot_bgcolor='#fff',
hovermode = 'x unified',
width = 650,
height = 320,
font = dict(size = 10),
margin=go.layout.Margin(l=50,
r=50,
b=60,
t=35))
plot(figb, filename = 'fig3_b.html', config = config)
display(HTML('fig3_b.html'))
Функцијата Вкупно е поставена за еден вид на тест за точноста на формулите, бидејќи збирот на S, E, I, R и D мора да биде еднаков на вкупната популација, т.е. $N = S(t)+E(t)+I(t)+R(t)+D(t)$, за било кое $t \in [0,100]$).
