Моделирање на заразна болест¶
Во последната година неочекувано се најдовме во ситуација во која науката за ширење и моделирање на заразни болести е од енормно значење за нас. На индивидуално ниво, сакаме и треба да знаеме што да очекуваме од карантин, вакцини и како ни влијае терапаијата што ни ја препишуваат матичните лекари. На ниво на популација пак, сакаме да знаеме како една зараза станува епидемија и потоа пандемија. Дефинитивно сакаме сигурност кога станува збор за чекорите врз кои ни се засновани стратегии за борба со вакви болести бидејќи многу животи се ризикуваат.
Но, науката не гарантира секогаш сигурност. Било кое научно достигнување е засновано зад модели што ги конструираме со цел да дознаеме повеќе за работите што не интересиират и екпсериментите што ги спроведуваме, независно дали моделите соодвестуваат со реалноста. Математичките модели се само карикатури од вистински системи и ситуации, имаат цел само да ги доловат фундаменталните механизми на процесите што доведува до објаснување (за набљудувања или предвидувања).
George Box [1919-2013]
“Essentially all models are wrong, but some are useful.” [1]
Иако за мене секогаш оваа изрека ќе биде првото предавање по предметот “Машинско учење” од акад. проф. Љупчо Коцарев, што познатиот статистичар Џорџ сака да опише е како моделите се сиромашни портрети на вистинскиот свет, независно нивната комплексност. Но, корисен модел може да ни даде многу вредни и корисни гледишта за проблеми кои не интересиират. Ни дозволуваат да ги разбираме и засноваме нашите одлуки врз инфромации наспроти шпекулации.
Заразни болести се доста голем товар на општественото здравство и економијата. Нови болести се појавуваат често, и стари болести мутираат и опстојуваат. Голема развновидност постои во пристапите на моделирање, почнувајќи од прости компараментални модели што претпоставуваат добро измешана популација поделена во неколку состојби (compartments) до агетно-базирани модели од големи размери што можат да симулираат движење на болест меѓу градови, континенти.
Овие прости модели ни дозволуваат аналитички да објаснуваме како примарните механизми влијаат на важни настани, како на пример дали епидемија ќе настане, колку долго би траела, која би била смрттната стапка, колку голема би била. Да ги добиеме овие едноставани објаснувања, компензираме многу на точноста што тоа што ги изоставаме сите секундарни ефекти (возраст на население, како вирусот се шири и слично). На другата страна пак, комплексните модели можеме да моделираме демографиски карактеристики, заедници, вакцни, карантини (lockdowns). Овие модели имаат многу поголема предвидувачка моќ, но нивната комплексност може да не ни даде толку голем увид во проблемот.
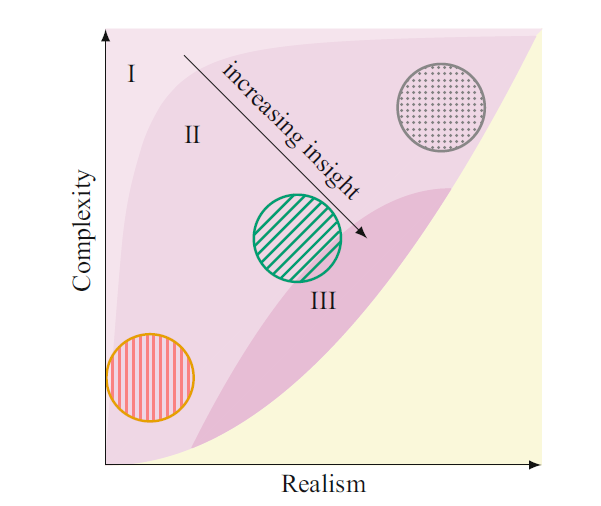
Првата фигура од книгата “Mathematics of Epidemics on Networks” многу добро ја доловува врската меѓу реалноста, комплексноста и увидот што моделот го спроведува. Фигурата покажува каде во ваква релација би стоеле едноставните компарементални модели (тие ние што ги користиме во проектот) - црвен круг лево; комплексни модели засновани на мрежи - зелен круг средина и агетно-базирани модели засновани на податоци (data-driven) - сив модел - десно.
[Mathematics of Epidemics on Networks] Fig 1.1.
Долниот лев регион не е до крај во жолто, т.е. е исклучен - тоа е минималната комплексност што е нужна за модел да долови одредено ниво на реалност. Увидот е лимитиран од самата комплекност на моделот (тоа што ни ја редуцира можноста да разбереме обични механизми) и реалноста (не можеме да учиме нешто за феномен што моделот не го вметнува во себе). Ако се движиме од светли (I) кон потемни региони (III) се зголемува и увидот што го добиваме. Очекуваме дека најголем увид би имале тогаш кога моделот содржи доволно компоненти да направи портрет на проблем (делумно реален) и во исто време е доволно комплексен да се разбере (делумно комплексен). Во реалноста, овие парадигми не би требало да се толку јасно одделни и дистинкцијата меѓу нив би требало да е помалку видлива.
Како што предлага фигурата, моделите спроведуваат максимален увид во проблемот кога има доволно рамнотежа, таму каде реалноста и едноставноста се среќаваат. Каде оваа рамнотежа лежи зависи само од природата на проблемот и ние сме должни да го одгвориме тоа прашање.