Алтернативна Power-law мрежа¶
Бидејќи сега знаеме дека структурата на мрежата може да влијае на начинот на однесување на болеста, очигледното прашање е точно каков е овој ефект. Поврзано прашање, нешто помалку апстрактно, е како овој ефект се манифестира на пореален модел на човечки контакти. Ако можеме да развиеме модел што имитира „реална“ социјална ситуација, можеме да се приближиме до тоа како може да се однесуваат вистинските епидемии.
За изненадување, моделирањето човечки контакти е доста тешко. Навистина, сè уште нема научен концензус за тоа какви видови мрежи се „најдобриот“ модел - и ова не само затоа што има многу различни социјални структури за кои треба да се смета.
Начините на кои луѓето се мешаат суштински се менуваат како што се зголемуваат географските и популационите размери, кога веќе не ги познавате соседите и кога патувате и мешате на пошироко подрачје. Дури и толку едноставна реченица имплицира многу математичка сложеност. Помалку мешање има во мал обем со соседите, но повеќе мешање на подолги растојанија со несоседите - и ова е пред да размислиме како мрежите на пријателство се меѓусебно поврзани и ефектите од контрамерките на болеста како што се социјалното дистанцирање што одеднаш станаа одлика на модерниот живот.
Доволно е да се каже дека студијата за мрежи за контакт е сè уште активно поле на истражување, спроведено експериментално со проучување на реални социјални мрежи како што се изложени на социјалните медиуми и теоретски со проучување на мрежи со тополошки структури кои се обидуваат да рефлектираат како луѓето комуницираат.
Додека „вистинскиот“ модел сè уште не е познат, сепак можеме да напредуваме користејќи го (што тврдиме дека е) подобар модел од едноставната мрежа за ER и да истражиме какви ефекти има.
Контакт кај физички мрежи¶
Човечките мрежи за контакт треба да ги моделираат структурите што всушност ги наоѓаме во човечките социјални структури. Овие структури се опширно проучувани и тие покажуваат огромна варијација - далеку повеќе отколку што наоѓаме во пример, структурата на мрежите во природните физички и биолошки системи. Ова е можеби заради разновидноста на културните фактори кои ги движат социјалните структури или можеби затоа што многу такви мрежи се дизајнирани за специфични цели, наместо едноставно да се развиваат по случаен избор.
Еден заеднички фактор е дека степенот на дистрибуција на контактната мрежа не е нормален (во математичка смисла) како оној на мрежата ЕР. Наместо бројот на контакти да се соберат околу одредена средина, имаме тенденција да набудуваме мал број на јазли кои се многу високо поврзани - далеку повеќе поврзани отколку што е можно во мрежата на ЕР. Овие луѓе понекогаш се нарекуваат хабови (hubs). Во моделирањето на болести, ови т.н. супер-распрснувачите може да бидат подобар израз: лица кои, доколку се заразат, потенцијално можат да заразат огромен број други. Ова има импликации врз контрамерките и вакцинацијата, имунитет на стадо и сл.
Контактните мрежи честопати ги хиперболизираат факторите кои се присутни во основната математика. Изберете јазол во мрежата по случаен избор и погледнете ги неговите соседи: какви би очекувале да бидат нивните степени? Излегува дека степени на соседи на јазоли избрани по случаен избор имаат тенденција да бидат поголеми од оние на самиот јазол. Тоа е затоа што има повеќе можности за поврзување со јазол кој има висок степен отколку со оној со низок степен (Pareto Principle). Ова е интересн експеримент што го имам спроведено за слична тематика, каде испитував на рандом синџири каква е дистрибуцијата на нивната должина.
Овој сличен феномен како тој на Парето, во социјална средина значи дека вашите пријатели се обично попопуларни од вас: тие, во просек, имаат повеќе пријатели од просекот. Ова важи за секој јазол избран по случаен избор - и така, парадоксално, додека твоите пријатели се во просек попопуларни од тебе, нивните пријатели исто така се просечно попопуларни од нив. Јасно е дека ова не може да важи за сите во истата мрежа и е уште еден пример за тоа како просечноста може да прикрие важни детали.
Потоа, тука е прашањето за случајност. Едно нешто што е очигледно во врска со мрежите за пријателство е дека тие имаат тенденција да не бидат случајни. Ако имате двајца пријатели, тие веројатно ќе бидат пријатели едни на други - иако не мора, бидејќи луѓето честопати имаат неповрзани под-групи на пријатели. Математички, ова се манифестира како кластери во мрежата кои се многу повеќе поврзани, што би се очекувало во случајно поврзана мрежа: всушност, зачудувачки е малку веројатно таквите структури да се појават во случајно изградена мрежа. Справувањето со ова групирање е математички многу предизвикувачко и претставува една од границите на тековните истражувања. Подобрите модели ќе го подобрат начинот на кој ги анализираме социјалните мрежи и ќе го подобриме потценувањето на процесите (како болести) што работат над нив.
Powerlaw мрежи¶
Тука веќе почнав повеќе да навлегувам во тематиката на мрежи не само на равенки. Има различни топологии како што спопнав и некои се пологични за решавање на некој проблем додека други за друг.Но, кај мрежите за контакт, се знае дека има некои луѓе кои имаат масовно повеќе контакти од други, или многу повеќе од просекот. Ова е пренесено во крајност на социјалните медиуми, каде што релативно мал број јавни и славни личности имаат милиони „пријатели“. И покрај тоа што овој поим за „пријателство“ е различен од „вистинското“ пријателство, ние гледаме слични ефекти во физичките мрежи за контакт: мрежите што фаќаат како луѓето комуницираат во реалниот свет.
Ова се случува на индивидуално социјално ниво, каде што некои луѓе се природно (или принудено) осамени, додека други се социјални пеперутки. Тоа се случува и преку фактори како што се работата, каде што некои луѓе - поштенски работници, касиери во продавници, возачи на автобуси, наставници - комуницираат со многу повеќе луѓе, и далеку поблиску, отколку со оние на други работни места.
Каква дистрибуција на степени имаат ваквите мрежи? Тие често го следат степенскиот закон (power law), каде што веројатноста јазолот да има одреден степен наликува на \(p_k \propto k^{-\alpha} \), за одреден степен \(\alpha > 0\). Овие power law мрежи ги опишуваат структурите на мрежите во збунувачки опсег на апликации: најпознато, тие ја опишуваат структурата на основното инженерство на Интернет и бројот на врски до веб-страници. Овие мрежи се нарекуваат и БА мрежи според нивните откривачи, и мрежи без размер (scale-free) бидејќи нивните големи и мали структури изгледаат исто.
Но, и Power law мрежите не се баш соодветни за контактните мрежи, бидејќи тие можат да создадат јазли со навистина, навистина високи степени: премногу високи за да се појават во човечки социјални ситуации.
За среќа има варијација на оваа идеја, проучена од Newman, Watts и Strogatz [15] и се покажала дека е многу подобра. Во овие мрежи, дистрибуцијата на степенот на моќ-закон може да биде „отсечена“ (cutoff) со одреден праг, ова се прави пред да може да стане преголема, во суштина поставувајќи ограничување на бројот на контакти што може да ги има една индивидуа. Овие мрежи се познати како powerlaw cutoff мрежи.
Градење на ваква мрежа¶
Градењето на ваква контактна мрежа веќе го имаше како готов формат (готови кодови), но јас се обидов да имитрам готови од различни тетратки со цел да демонстрирам моделирање. Идејата е оваа изградба на мрежа да резултира со мрежа каде што јазлите имаат точна дистрибуција на степен. Со други зборови, јазлите во мрежата со степен \(k\) се појавуваат во дел предвидена со дистрибуцијата на степенот.
Кога конструиравме EР мрежа, опишавме алгоритам кој, кога се следи, произведува мрежа со посакувана дистрибуција. Потребен ни е различен алгоритам за ракување со овие различни топологии. Излегува дека постои многу општ алгоритам, наречен конфигурациски модел (configuration model), што може да конструира случајна мрежа со која било дистрибуција на степени.
За да се изгради мрежа со големина \(N\), конфигурацискиот модел зема список со \(N\) броеви, секој опишува степен на јазол. Создава јазли со овие степени и ги поврзува нивните рабови случајно. Ако можеме да ја креираме низата степени што ја сакаме од дистрибуцијата на степени, можеме да го користиме моделот за конфигурација за да изградиме случајна мрежа со јазли што ги имаат тие степени.
Ние дефинираме функција која, на даден степен \(k\), ја враќа веројатноста \(p_k\) на јазолот со тој степен да се појави во мрежата. Потоа дефинираме друга функција на која и ја обезбедуваме оваа функција какво влез, заедно со бројот на јазли што ги сакаме и која создава случајна мрежа. Постојано се избира случаен степен и потоа се избира случаен број помеѓу 0 и 1 (слично како кај EР мрежите). Ако овој втор број е помал од веројатноста на јазол со настанување на тој степен, тој го додава степенот на низата; во спротивно, тој го повторува процесот за друг степен. Ова продолжува сè додека не имаме степени на \(N\) јазол, а потоа можеме да преминеме на моделот за конфигурација за да се поврземе заедно.
def generateFrom(N, p, maxdeg=100):
# конструирај степени согласно со дистрибуцијата дадена
# од функцијата модел p()
rng = numpy.random.default_rng()
ns = []
t = 0
for i in range(N):
while True:
# цртај рандом степен
k = rng.integers(1, maxdeg)
# дали го додаваме овој степен на овој јазел?
if rng.random() < p(k):
# да, додади го во секвенцата; инаку,
# цртај повторно
ns.append(k)
t += k
break
# последната низа на степени треба да се сумира на еднаквост
# број, бидејќи секој раб има две крајни точки
# ако низата е непарна, отстранете елемент и нацртајте
# друг од дистрибуцијата, повторувајќи сè до
# целокупната низа е рамномерна
while t % 2 != 0:
# бирај јазол случајно
i = rng.integers(0, len(ns) - 1)
# острани го од секвенцата и од total
t -= ns[i]
del ns[i]
# избери јазол кој го заменува отстранетиот
while True:
# исцртај нов степен од дистрибуцијата
k = rng.integers(1, maxdeg)
# дали да вклучиме јазол со овој степен?
if rng.random() < p(k):
# да, додади го во секвенцата; инаку,
# цртај повторно
ns.append(k)
t += k
break
# населете ја мрежата користејќи ја конфигурацијата
# модел со дадената дистрибуција на степен
g = networkx.configuration_model(ns,
create_using=networkx.Graph())
return g
Сега треба да ја опишеме дистрибуцијата на законот за напојување со намалување на степенот. Математички, веројатноста да наидете на јазол од степен \(k\) под оваа дистрибуција е дадена со:
Бидејќи дистрибуцијата е опишана со два параметра - степенот \(\alpha\) и cutoff \(\kappa\) - ние дефинираме функција што ги зема овие два параметра и враќа функција што враќа \(p_k\) за кој било степен \(k\).
def makePowerlawWithCutoff(alpha, cutoff):
C = 1.0 / mpmath.polylog(alpha, numpy.exp(-1.0 / cutoff))
def p(k):
return (pow((k + 0.0), -alpha) * numpy.exp(-(k + 0.0) / cutoff)) * C
return p
Потоа можеме да ја покажеме дистрибуцијата на степенот што резултира, со повторно создавање мрежа и потоа цртање на хистограм на степени на јазли.
# мала мрежа + параметри
N = 10000
alpha = 2
cutoff = 40
# генерирање на мрежата од параметрите што ги опишуваат
# дистрибуција на степени
g = generateFrom(N, makePowerlawWithCutoff(alpha, cutoff))
fig = plt.figure(figsize=(7, 7))
ax = fig.gca()
# исцртај ја степенската дистрибуција
ks = list(dict(networkx.degree(g)).values())
ax.hist(ks, bins=max(ks), color='green')
ax.set_title('Алтернативна Powerlaw мрежа; degree distribution ($N = {n}, \\alpha = {e}, \\kappa = {k}$)'.format(n=N, e=alpha, k=cutoff), y=1.05)
ax.semilogy()
ax.set_xlabel('$k$')
ax.set_ylabel('$\\log \\, N_k$')
plt.show()
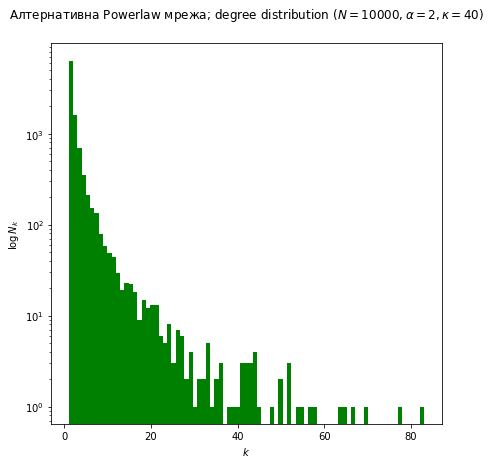
Може да се забележи дека бројот на јазли паѓа експоненцијално се додека не го погоди просекот (40), по што станува навистина редок: има многу малку јазли со степени поголеми од вредноста на просекот.