Транзиции на состојби¶

Во претходната секција ги разгледувавме параметрите кои влегуваат во почетно моделирање на заразни болести. Во оваа секција ќе разгледуваме истиот модел но од различен - (по) визуелен агол, т.е. ќе ги разгледаме следните проширувања на основниот модел:

Состојба “Починати” → \(D(t)\), за индивидуи кои починале од заразата
Состојба “Изложени” → \(E(t)\), за индивидуи кои стаипле во контакт со заразната болест меѓутоа сеуште не се заразливи (познато и како SEIR модел)
Временски зависни \(R_0\) вредности што ни овозможуваат да моделираме карантин, комплетни изолации и сл.
Возрасно и ресурсно зависни стапки на смртност, што ни возможуваат да моделираме популации со многу млади/возрасни луѓе, преокупирани болници и сл.

Модели како транзиции на состојби¶

Краток преглед на променливите кои досега ги дефиниравме:

\(N\): вкупна популација
\(S(t)\): здрави во време \(t\) од започнување на епидемијата
\(I(t)\): инфицирани во време \(t\) од започнување на епидемијата
\(R(t)\): оздравени во време \(t\) од започнување на епидемијата
\(\beta\): очекуваниот број на луѓе на кои заразена личност ја пренесува болеста
\(D\): бројот на денови што личноста ја чува во себе и може да ја шири болеста
\(\gamma\): бројот на заразени личности што заздравуваат на ден (\(\gamma= \frac{1}{D}\))
\(R_{0}\): вкупниот број на луѓе кој една личност заразува (\(R_{0}=\beta \cdot D\))

Основните диференцијални равенки:

\[\begin{align*} \frac{dS}{dt} &= -\beta \cdot I \cdot \frac{S}{N} \\ \frac{dI}{dt} &= \beta \cdot I \cdot \frac{S}{N} - \gamma \cdot I \\ \frac{dR}{dt} &= \gamma \cdot I \end{align*}\]

Во изведувањето на равенките, интиутивно ги разгледавме формулите како насоки што ни кажуваат што ќе се случи со популацијата следниот ден (на пр., кога 10 луѓе се заразени (\(I\)) и времето потребно за оздравување е со рата \(\frac{1}{5}\) (\(\gamma\)), тогаш бројот на оздравени луѓе следниот ден треба да се зголеми за \(\frac{1}{5}\cdot 10 = 2\)).

Сега нашето разбирање за овие равенки како насоки или транзиции од едена состојба S, I или R во друга ќе го потврдиме со следните анализи. Ова воведување на транизиции од една во друга состојба ќе ни озвозможи поголема прегледност при рабоотење со равенките кога ќе воведеме повеќе параметри.

Состојби се вакви кругови:

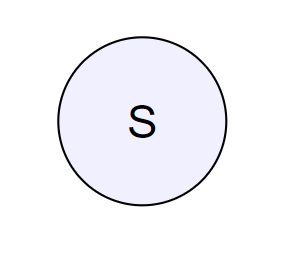
Fig. 3 Единечна состојба S¶

Од овие транзиции ги изведуваме следните равенки:

\[\begin{align*} \frac{dS}{dt} &= -\beta \cdot I \cdot \frac{S}{N} \\ \frac{dE}{dt} &= \beta \cdot I \cdot \frac{S}{N} - \delta \cdot E \\ \frac{dI}{dt} &= \delta \cdot E - \gamma \cdot I \\ \frac{dR}{dt} &= \gamma \cdot I \end{align*}\]

Транзиции од една состојба во друга се претставени со стрелки, со следната нотација:

Fig. 4 Визуелен приказ на производот од стапката, веројатноста, популацијата¶

Од овие транзиции ги изведуваме следните равенки:

\[\begin{align*} \frac{dS}{dt} &= -\beta \cdot I \cdot \frac{S}{N} \\ \frac{dE}{dt} &= \beta \cdot I \cdot \frac{S}{N} - \delta \cdot E \\ \frac{dI}{dt} &= \delta \cdot E - \gamma \cdot I \\ \frac{dR}{dt} &= \gamma \cdot I \end{align*}\]

Стапката го претставува времето потребно за една транзиција, веројатноста е еднаква на веројатноста оваа транзиција да настане за една индивидуа и популацијата е групата на луѓе на кои се однесува транзицијата.

Пример сценарио
Разгледуваме една транзиција од Подлежни (\(S\)) во Заразени (\(I\)) во нашите SIR равенки, каде ни се дадени следните почетни параметри:

\(\beta = 2\)
\(N=100\) (10 зразени, 90 подлежни)

Доколку стапката на пренесување на заразата е 1, како што заразувањата започнуваат веднаш; популацијата на која оваа транзиција се однесува е \(2\cdot 10 = 20\) индивидуи, секој еден од овие 10 заразени заразува уште 2 други подлежни; веројатноста е 90% (\(\frac{90}{100}\)) за подлежните да се заразат.

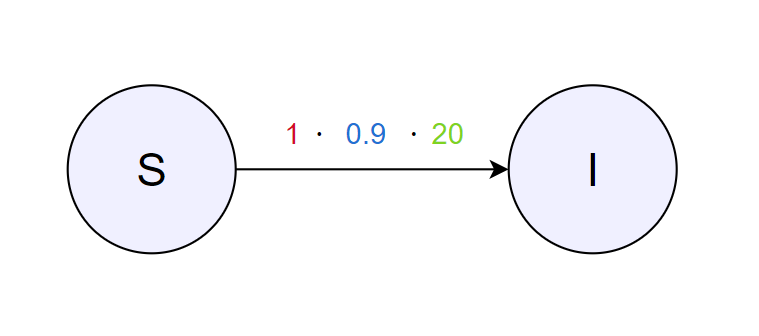
Fig. 5 Визуелен приказ на пример од производ¶

Генерално доколку ги напишеме сите транзиции кои настануваат од нашите равенки за целиот модел (\(I\rightarrow R\), каде \(\gamma\) е стапката веројатноста е 1 додека сите оздравуваат):

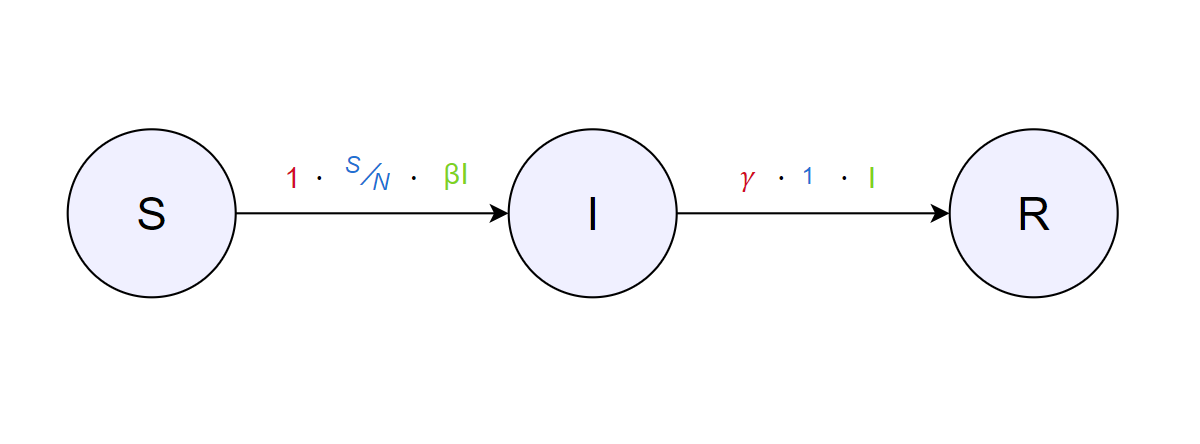
Fig. 6 Генерален запис за сите транизиции за SIR модел¶

\[\begin{align*} \frac{dS}{dt} &= -\beta \cdot I \cdot \frac{S}{N} \\ \frac{dI}{dt} &= \beta \cdot I \cdot \frac{S}{N} - \gamma \cdot I \\ \frac{dR}{dt} &= \gamma \cdot I \end{align*}\]

Можеме да заклучиме од последниот трансформатор, стрелките што покажуваат од една состојба во друга се додаваат во равенката; стрелките кои покажуваат надвор од една состојба се одземаат.

Сега и покрај ова моделирање на состојби како и моделите испрограмирани во Python ние сеуште сме далеку од моделирање на вистински податоци што кружат на интернет. Во оваа моментална состојба овој модел само ни овозможува да разгледаме во какви меѓусебни транзиции влегуваат одредени параметри и какво е нивното влијание преку време.

Имунитет на стадо

Транзиции на состојби¶

Модели како транзиции на состојби¶